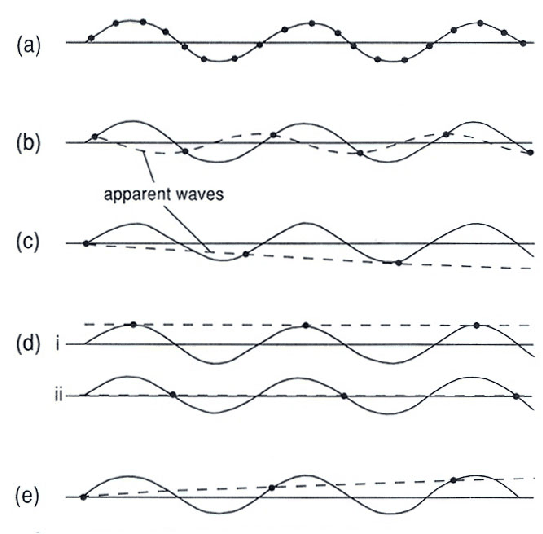
Fig 5.1: El efecto de alisado para una señal con mal muestreo.
La frecuencia de onda crítica, la mitad de la frecuencia de muestreo, es llamada frecuencia Nyquist. El alisado puede ocurrir para señales que contienen frecuencias cercanas de la frecuencia Nyquist.

Genere una señal en SAC de una onda seno, frecuencia 10 Hz, 100 muestras por segundo con una duración de 10 segundos. Use el comando interpolate para cambiar la delta de la señal así:
interpolate delta 0.02Prueba otras valores en la interpolación de 0.04, 0.08, 0.16 para ver lo que pasa a la señal cuando se pasa la límite Nyquist.
Filtros solo permiten un cierto rango de frecuencias pasar, para
acentuar la amplitud de la señal sísmica en comparación con el ruido.
Mientras que filtros son convoluciones en el dominio de tiempo, son una
multiplicación en el dominio de frecuencia. Se puede ver la forma de
filtros en el dominio de frecuencia cuando se aplica el filtro a una
función delta.
Genere una función delta en SAC, con alto muestreo, 10 segundos de largo. Ahora vamos a aplicar un filtro Butterworth a la función delta:
bandpass corner 2 4 npoles 6 passes 1Este filtro tiene frecuencias de esquina de 2 y 4 Hz, se construye con 6 polos, y se aplica con 1 paso. Grafique la función delta después de la aplicación del filtro. Luego, tome la transformada de Fourier de la señal (parte amplitud), para ver el rango de frecuencias en la señal que permite pasar el filtro.
El filtro Butterworth bandpass tiene una construcción matemática
bastante complicada, pero para ver el efecto visual del filtro siempre
se puede ver como modifica una función delta. Prueba el filtro de
nuevo, pero con (i) 2 polos, y (ii) 10 polos. ¿Cuál es el efecto de la
cantidad de polos en el filtro?
Bajen los siguientes archivos del sitio web:
http://www.mttmllr.com/ADS/DATA/
Ultimamente, encuentre un filtro aceptable para acentuar la onda S.
1) Usa el comando interpolate para reducir el muestreo de los sismogramas de la sección 5.3. ¿Cuál es la frecuencia de muestreo
límite con la cual se puede identificar bien el tiempo de llegada de la onda P?
2) Existen otros filtros además que bandpass. Ver el efecto de los siguientes filtros a una función delta: highpass, lowpass, bandrej.
This document was generated using the LaTeX2HTML translator Version 2008 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -nonavigation sac_05_filters.tex
The translation was initiated by matt on 2015-09-30