2 SAC - Polos y Ceros

2.1 Resumen de comandos

Hasta ahora, hemos visto algunos comandos para leer, generar y manipular series de tiempo. Un resumen de ellos se encuentra en la lista siguiente. Todos los comandos del programa SAC se puede encontrar en su pagina web:
http://ds.iris.edu/files/sac-manual/commands/alpha_commands.html

Datos

read (r) - Leer datos de archivos .sac

read more (r more) - Leer mas archivos de .sac juntos con lo que es ya leído

readtable - Leer archivos alfanuméricos

funcgen - Generar una función simple

write (w) - Escribir datos en la memoria a un archivo

listhdr (lh) - Mostrar los encabezados de las series de tiempo

chnhdr (ch) - Cambiar valores en el encabezado

writehdr (wh) - Guardar los valores del encabezado al archivo

Graficar

qdp - Control de la opción 'quick and dirty plot'

begindevices (bd) - Elegir el formato del gráfico: xw (x-window) o sgf (sac graphics format)

sgftops - Convertir un gráfico sgf a ps (postscript)

plot (p) - Graficar una traza por hoja

plot1 (p1) - Graficar múltiples trazas en una hoja

plot2 (p2) - Graficar múltiples trazas sobrepuestos en una hoja

plotpk (ppk) - Graficar y editar, use x para zoom in, o para zoom out, q para salir

Operaciones

add - Hacer una adición en cada punto en la serie de tiempo

sub/mul/div - Sustracción, multiplicación, división

sqr - Cuadrado

sqrt - Raíz cuadrada

abs - Valor absoluto

log - Logarítmico

log10 - Logarítmico en base 10

exp - Exponencial

exp10 - Exponencial,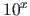

int - Integración de las series de tiempo

dif - Diferenciación

merge - Pegar dos series de tiempo juntos

addf - Sumar dos series de tiempo

subf - Sustraer una serie de una otra

mulf - Multiplicar dos series de tiempo

divf - Dividir una serie por una otra

interpolate - Interpolación de delta (el muestreo)

quit (q) - Salir del SAC

Datos
read (r)	- Leer datos de archivos .sac
read more (r more)	- Leer mas archivos de .sac juntos con lo que es ya leído
readtable	- Leer archivos alfanuméricos
funcgen	- Generar una función simple
write (w)	- Escribir datos en la memoria a un archivo
listhdr (lh)	- Mostrar los encabezados de las series de tiempo
chnhdr (ch)	- Cambiar valores en el encabezado
writehdr (wh)	- Guardar los valores del encabezado al archivo
Graficar
qdp	- Control de la opción 'quick and dirty plot'
begindevices (bd)	- Elegir el formato del gráfico: xw (x-window) o sgf (sac graphics format)
sgftops	- Convertir un gráfico sgf a ps (postscript)
plot (p)	- Graficar una traza por hoja
plot1 (p1)	- Graficar múltiples trazas en una hoja
plot2 (p2)	- Graficar múltiples trazas sobrepuestos en una hoja
plotpk (ppk)	- Graficar y editar, use x para zoom in, o para zoom out, q para salir
Operaciones
add	- Hacer una adición en cada punto en la serie de tiempo
sub/mul/div	- Sustracción, multiplicación, división
sqr	- Cuadrado
sqrt	- Raíz cuadrada
abs	- Valor absoluto
log	- Logarítmico
log10	- Logarítmico en base 10
exp	- Exponencial
exp10	- Exponencial,
int	- Integración de las series de tiempo
dif	- Diferenciación
merge	- Pegar dos series de tiempo juntos
addf	- Sumar dos series de tiempo
subf	- Sustraer una serie de una otra
mulf	- Multiplicar dos series de tiempo
divf	- Dividir una serie por una otra
interpolate	- Interpolación de delta (el muestreo)
quit (q)	- Salir del SAC

2.2 Funciones de prueba

En esta sección, generamos unas funciones sintéticas de prueba, para ver después lo que actualmente miden sismómetros si el suelo se esta moviendo en esta manera (Al final de esta clase, ponemos datos reales para su diversión).

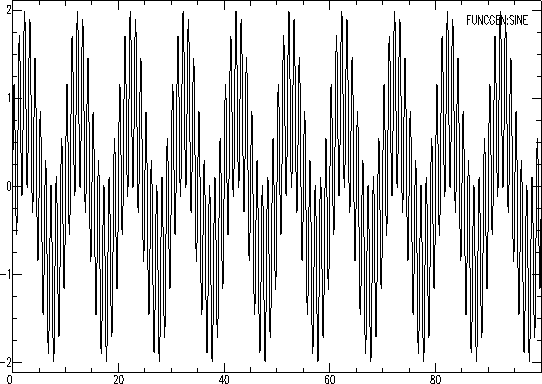
1) Generamos una señal que es una mezcla de senos de frecuencias de 1 Hz y 0.1 Hz.

SAC> funcgen sine 0.1 0 delta 0.01 npts 10000
SAC> w temp.sac
SAC> funcgen sine 1 0 delta 0.01 npts 10000
SAC> addf temp.sac
SAC> w sen1-0.1Hz.sac

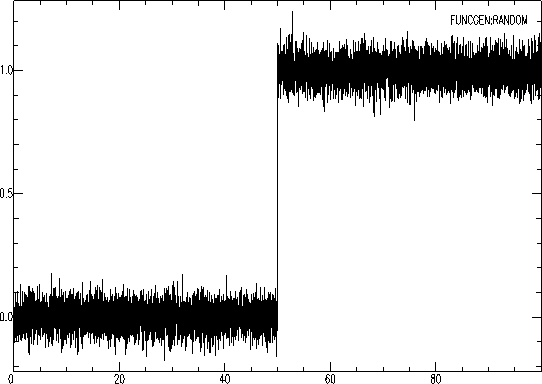
2) Generamos una señal que es una función de escalón con ruido.

SAC> funcgen step delta 0.01 npts 10000
SAC> w temp2.sac
SAC> funcgen random 1 delta 0.01 npts 10000
SAC> div 20
SAC> addf temp2.sac 
SAC> w escalon_ruido.sac

Fig 2.1: sen1-0.1Hz.sac

Fig 2.2: escalon_ruido.sac

2.3 Una transferencia con polos y ceros

Supongo que queremos poner la respuesta de un instrumento a una serie de tiempo (que representa desplazamiento del suelo). Es posible hacerlo usando la función de transferencia del instrumento, representado por sus polos y ceros (y un constante). En SAC, el comando ``transfer'' es usado por eso.

SAC tiene las funciones de transferencia de algunos sismómetros famosos en su programa, como lo de Wood-Anderson (wa). Podemos entonces ver lo que medirá este sismómetro, si el suelo era oscilando en la forma de una suposición de dos senos de 1 y 0.1 Hz (sen1-0.1Hz.sac). En el código que sigue, la función transfer convierte la señal de ``none'' a ``wa''. El ``none'' es desplazamiento del suelo en metros, alternativamente podemos usar ``vel'' para velocidad y ``acc'' para aceleración.

SAC> r sen1-0.1Hz.sac
SAC> transfer from none to wa
 Station (-12345  ), Channel (-12345  )
SAC> ppk

El sismómetro Wood-Anderson es analógico. Entonces la escala de la señal que registra el instrumento esta dada en el movimiento de la lápiz en el brazo del instrumento en milímetros.

¿Cuál es la diferencia entre la señal original, y lo que registra este instrumento?

Ahora vemos la respuesta de un sismómetro más moderno a la misma señal. El Güralp-40T. Tenemos que usar un archivo de sus polos y ceros (se puede obtener eso del manual del instrumento). El archivo 40T.pz tiene los polos, ceros y el constante para la función de transferencia; en SAC usamos la convención de radianes (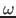) y desplazamiento (m). Aquí son los contenidos del archivo 40T.pz:

ZEROS 3
0 0
0 0
0 0
POLES 5
-0.148 -0.148
-0.148 0.148
-1130.97 0.0000
-1005.30 0.0000
-502.65 0.0000
CONSTANT 7.16e+17

Y ahora vemos la señal sen1-0.1Hz.sac registrado en este instrumento:

SAC> r sen1-0.1Hz.sac
SAC> transfer from none to polezero subtype 40T.pz
 Station (-12345  ), Channel (-12345  )
 Using polezero response for , , , ...
SAC> ppk

Ahora la escala vertical esta en cuentas (Volts) Se puede ver que el instrumento Güralp puede registrar la oscilación a 0.1 Hz mejor que el instrumento Wood-Anderson.

Ahora vean la respuesta del instrumento Güralp al archivo sen1-0.1Hz.sac suponiendo que el archivo representa la velocidad del suelo. La señal que mide este sismómetro representa velocidad del suelo, y debe tener una ganancia aproximadamente lineal entre 0.03 y 50 Hz, entonces debe ser muy poca diferencia en la velocidad del suelo, y el registro del instrumento.

Si hay tiempo, es posible a hacer este análisis sobre el archivo escalon_ruido.sac.

2.4 Extraer el efecto del instrumento

Bajen el archivo murta.sac que muestra una onda-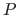 telesísmica registrado en un instrumento Güralp-40T. Si quieren saber los detalles de la estación y del sismo, se puede ver el encabezado.

Fig 2.3: murta.sac.

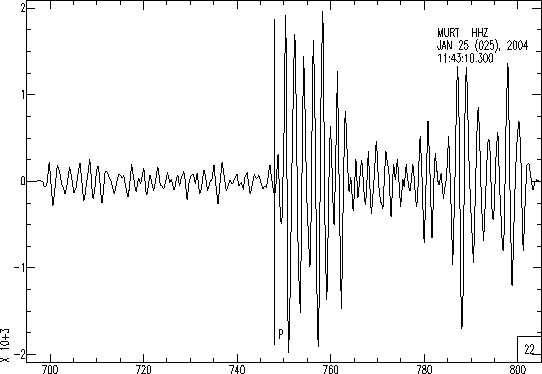
Por ahora, la señal es lo que mide el instrumento. Si queremos extraer la respuesta del instrumento, podemos usar el comando ``transfer'' en la misma manera que la sección anterior:

SAC> r ./murta.sac 
SAC> transfer from polezero subtype 40T.pz to none
 Using polezero response for MURT, HHZ, XJ, ...
 Station (MURT    ), Channel (HHZ     )
SAC> p1

¿Cuál es el desplazamiento (en mm) de la onda-P en esta estación?

Hacer una transferencia al desplazamiento, y una diferenciación de la señal con ``dif'' para llegar a la velocidad. Revisen que lo que se obtiene es la misma señal que si uno se hace la transferencia directamente a velocidad.

Si hubo un sismómetro Wood-Anderson registrando la onda, en vez del 40T, ¿que señal registrará?

2.5 La transformada de Fourier

En SAC podemos hacer una transformada de Fourier a la señal usando ``fft'' (fast Fourier transform). Esta transformada tiene información de amplitud y fase. Para guardar solamente la parte de la amplitud, usamos ``keepam'' (keep amplitude). Hagamos esta operación a la señal sen1-0.1Hz.sac:

SAC> r sen1-0.1Hz.sac 
SAC> fft
 DC level after DFT is 1.9091e-05
SAC> keepam
SAC> xlim 0.01 2
SAC> p1

Noten que aquí el comando ``xlim'' denota los límites del eje-x.

Fig 2.4: El espectro de frecuencia de sen1-0.1Hz.sac.

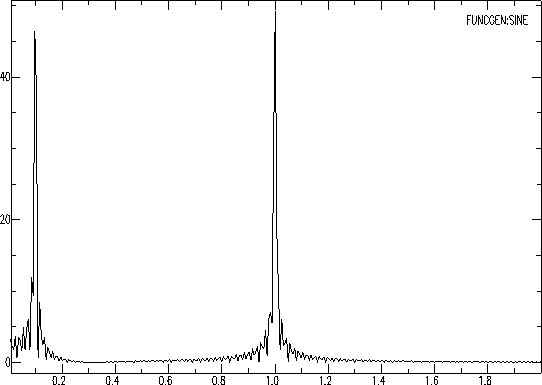
Si ponemos la respuesta de velocidad de un sismómetro Wood-Anderson a esta señal original, ¿cómo cambiará el espectro de frecuencia?

También podemos usar la transformada de Fourier para ver la respuesta (en términos de amplitud) de un instrumento directamente de su archivo de polos y ceros. Por eso, debemos ver la respuesta del instrumento a una señal impulsiva en el dominio de frecuencia:

SAC> funcgen impulse delta 0.0001 npts 1000000
SAC> transfer from vel to polezero subtype 40T.pz
 Station (-12345  ), Channel (-12345  )
 Using polezero response for , , , ...
SAC> fft
 DC level after DFT is -24.625
SAC> keepam
SAC> xlog
SAC> xlim 0.001 1000
SAC> p1

Aquí, el comando ``xlog '' pone la escala-x logarítmica.

En este gráfico, podemos ver lo que significa cuando Güralp dicen que su instrumento tiene una respuesta lineal en velocidad entre 50 Hz y 30 s. El instrumento es desarrollado para medir ondas sísmicas y representar la velocidad del suelo en este rango de frecuencia.

Fig 2.5: La ``ganancia'' del instrumento 40T a diferentes frecuencias.

Haga el mismo tipo de análisis para el sismómetro Wood-Anderson, para ver dentro de que rango de frecuencia puede medir las ondas.

About this document ...

This document was generated using the LaTeX2HTML translator Version 2008 (1.71)

The command line arguments were:
latex2html -split 0 sac_02_pz.tex

The translation was initiated by matt on 2012-08-25

matt 2012-08-25